suku banyak
Suku Banyak
Suku banyak atau polinominal merupakan pernyataan matematika yang melibatkan penjumlahan perkalian
pangkat dalam satu atau lebih variable dengan koefisien. Bisa dibilang
polinominal merupakan bentuk aljabar dengan pangkat peubah bilangan bulat
positif. Suku banyak dalam x berderajat n mempunyai bentuk umum:
§ dan
dan 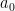 adalah
konstanta real
adalah
konstanta real
§ 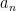 koefisien
koefisien  koefisien
koefisien 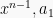 koefisien
koefisien 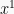 dan
seterusnya
dan
seterusnya
§ 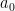 disebut suku tetap
disebut suku tetap
§ n bilangan cacah yang
menyatakan derajat suku banyak
Nilai Suku Banyak
Suku banyak dalam x
berderajat n dapat ditulis dalam bentuk fungsi sebagai berikut:
Nilai  untuk
untuk  adalah
adalah 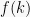 . Nilainya
dapat ditentukan dengan dua strategi, yaitu:
. Nilainya
dapat ditentukan dengan dua strategi, yaitu:
Substitusi
Misalkan nilai 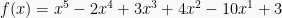 untuk
untuk  dengan
dengan  dapat
ditentukan dengan mensubstitusi menjadi:
dapat
ditentukan dengan mensubstitusi menjadi:
Komentar
Posting Komentar