perkalian matriks

Perkalian Matriks

Matriks dapat dikalikan dengan sebuah bilangan bulat atau dengan matriks lain. Kedua perkalian tersebut memiliki syarat-syarat masing-masing.

Perkalian Matriks dengan bilangan bulat

Suatu matriks dapat dikalikan dengan bilangan bulat, maka hasil perkalian tersebut berupa matriks dengan elemen-elemennya yang merupakan hasil kali antara bilangan dan elemen-elemen matriks tersebut. Jika matriks A dikali dengan bilangan r, maka 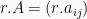r.A = (r.a_{ij}). Contoh:
Jika 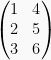\begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{pmatrix} dan bilangan r = 2, maka:
r.A = 2 . \begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{pmatrix} = \begin{pmatrix} 2.1 & 2.4 \\ 2.2 & 2.5 \\ 2.3 & 2.6 \end{pmatrix} = \begin{pmatrix} 2 & 8 \\ 4 & 10 \\ 6 & 12 \end{pmatrix}
Perkalian matriks dengan bilangan bulat dikombinasikan dengan penjumlahan atau pengurangan matriks dapat dilakukan pada matriks dengan ordo sama. Berikut sifat-sifat perkaliannya:
  • r(A + B) = rA + rB
  • r(A – B) = rA – rB

Komentar

Posting Komentar

Postingan populer dari blog ini

contoh soal trigonometri

Gambar
Soal No. 1 Nyatakan sudut-sudut berikut dalam satuan derajad: a)  1 / 2  π rad b)  3 / 4  π rad c)  5 / 6  π rad Pembahasan Konversi: 1 π radian = 180° Jadi: a)  1 / 2  π rad b)  3 / 4  π rad c)  5 / 6  π rad Soal No. 2 Nyatakan sudut-sudut berikut dalam satuan radian (rad): a) 270° b) 330° Pembahasan Konversi: 1 π radian = 180° Jadi: a) 270° b) 330° Soal No. 3 Diberikan sebuah segitiga siku-siku seperti gambar berikut ini. Tentukan: a) panjang AC b) sin θ c) cos θ d) tan θ e) cosec θ f) sec θ d) cotan θ Pembahasan a) panjang AC Dengan phytagoras diperoleh panjang AC b) sin θ c) cos θ d) tan θ e) cosec θ f) sec θ g) cotan θ Soal No. 4 Sebuah segitiga siku-siku. Diketahui nilai dari sin β =  2 / 3 . Tentukan nilai dari : a) cos β b) tan β Pembahasan sin β =  2 / 3  artinya perbandingan panjang sisi depan dengan sisi miringnya adalah 2 : 3 Gunakan phytagoras untuk menghitung panjang sisi yang ketig...
Baca selengkapnya

contoh soal induksi matematika

  Soal Nomor 1 Buktikan dengan  induksi  matematika bahwa P n : 1 + 2 + 3 + ⋯ + n = n ( n + 1 ) 2 P n : 1 + 2 + 3 + ⋯ + n = n ( n + 1 ) 2 bernilai benar untuk setiap  n n   bilangan asli . soal nomor 2 soalSoal Nomor 2 Buktikan bahwa  2 + 4 + 6 + ⋯ + 2 n = n 2 + n 2 + 4 + 6 + ⋯ + 2 n = n 2 + n untuk  n n   bilangan asli Soal Nomor 3 Buktikan dengan  induksi  matematika bahwa P n : 1 2 + 2 2 + 3 2 + ⋯ + n 2 = n ( n + 1 ) ( 2 n + 1 ) 6 P n : 1 2 + 2 2 + 3 2 + ⋯ + n 2 = n ( n + 1 ) ( 2 n + 1 ) 6 bernilai benar untuk semua  n n   bilangan asli . Soal Nomor 4 Buktikan dengan  induksi  matematika bahwa P n : 1 + 3 + 5 + ⋯ + ( 2 n − 1 ) = n 2 P n : 1 + 3 + 5 + ⋯ + ( 2 n − 1 ) = n 2 bernilai benar untuk setiap  n n   bilangan asli . Soal Nomor 5 Buktikan dengan  induksi  matematika bahwa P n : 1.2 + 2.3 + 3.4 + ⋯ + n ( n + 1 ) = n ( n + 1 ) ( n + 2 ) 3 P n : 1.2 + 2.3 + 3.4 + ⋯ + n ( n +...
Baca selengkapnya

suku banyak

Gambar
Suku Banyak Suku banyak  atau polinominal merupakan pernyataan  matematika  yang melibatkan penjumlahan perkalian pangkat dalam satu atau lebih variable dengan koefisien. Bisa dibilang polinominal merupakan bentuk aljabar dengan pangkat peubah bilangan bulat positif. Suku banyak dalam x berderajat n mempunyai bentuk umum: §  dan   adalah konstanta real §     koefisien   koefisien   koefisien   dan seterusnya §      disebut suku tetap §   n bilangan cacah yang menyatakan derajat suku banyak Nilai Suku Banyak Suku banyak dalam x berderajat n dapat ditulis dalam bentuk  fungsi  sebagai berikut: Nilai   untuk   adalah  . Nilainya dapat ditentukan dengan dua strategi, yaitu: Substitusi Misalkan nilai   untuk   dengan   dapat ditentukan dengan mensubstitusi menjadi:
Baca selengkapnya